Оригами № 1(27) 2001
Пирамиды Зачем строили пирамиды? Существующее ещё с античных времён мнение о пирамидах как о гигантских надгробиях, скрывающих могилы знатных погребённых, а значит, и несметные сокровища, служило приманкой для многочисленных грабителей. Сколько поколений алчных гробокопателей-исследователей за всю многовековую историю существования пирамид надорвало своё здоровье и погибло в их недрах, никто не знает. Нет достоверных сведений из мрака времён и о тех ценностях, которые могли бы быть выкрадены. Тысячелетиями пирамиды гордо хранят молчание о своём происхождении и предназначении. Но любопытство человека к этим творениям не ослабевает, и каждый год влечёт многочисленных туристов поглазеть на пирамиды. По обилию пирамид, приходящихся на сравнительно небольшую площадь, несомненно, ведёт Египет (фото 1). Комплекс пирамид в Гизе - настоящая Мекка для любознательных паломников. Но пирамиды или их остатки есть в Индии, Пакистане, Индонезии, на Мальдивских и Канарских островах, в Китае, Южной и Латинской Америке (Американский материк вообще первенствует по количеству пирамид и их размерам)... Более тридцати пирамид есть и на землях России! Правда, в отличие от вышеперечисленных пирамид, самой «древней» российской пирамиде около пяти лет, а самая молодая была построена в Подмосковье (ок. 50 км. от Москвы по Новорижскому шоссе) в конце 2000 года и имеет высоту всего 44 метра.
Фото 1 Рис. 1
Подавляющее большинство пирамид имеет ступенчатую форму (фото 2). Правильные, вроде Великих пирамид в Гизе (Хеопса, Хефрена и Микерина), строили редко. Но даже там из трёх пирамидок-спутниц пирамиды Микерина две ступенчатые. Кроме того, все правильные пирамиды усечены, т. е. как бы недостроены, не имеют остроконечной вершины и заканчиваются плоской площадкой. Исследователи пирамид теряются в догадках, почему пирамиды не имеют верхушки и для каких целей служили площадки?
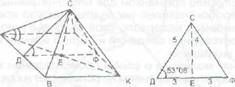
Рис. 2	Фото 2.
Ступенчатая мини-пирамида-мавзолей на Красной площади в Москве (фото 3) по своим размерам не идёт ни в никакое сравнение с древними пирамидами египтян и ацтеков. Однако Мавзолей не менее известен и популярен в мире. Ведь он не только пирамида, но ещё и усыпальница, где в особом саркофаге уже около восьмидесяти лет сохраняется мумия Ленина! Архитектор А. В. Щусев дважды перестраивал деревянный Мавзолей-пирамиду, прежде чем в октябре 1930 года появился окончательный, третий - каменный его вариант. Первоначальный замысел и проект претерпели незначительные изменения - были учтены все пожелания соратников вождя (Л. Б. Красина и А. В. Луначарского) и на ступенчатой пирамиде-усыпальнице появилась трибуна...
Фото З.
Не обошлись без пирамиды и отцы-основатели США. Правда, до строительства дело не дошло, а ограничилось только принятием Конгрессом США в 1776 году эскиза государственной печати с усечённой пирамидой. Если посмотреть на американскую купюру достоинством в 1 доллар (на которой портрет Вашингтона), то на её обороте и сейчас можно видеть эту печать (фото 4) пирамиду со срезанной вершиной, а над ней парящий треугольник с глазом в центре.
Кстати, современные российские пирамиды тоже усечены. Это, пожалуй, единственное, что объединяет новострой с древними архитектурными памятниками. В отличие от своих предшественниц, сложенных из каменных блоков, современные пирамиды имеют пирамидальный каркас, выложенный снаружи плитами из стеклопластика. Разный принцип заложен и в геометрию египетских и российских пирамид. Строители Великих пирамид, скорее всего, брали за основу прямоугольный треугольник с соотношением сторон 3 : 4 : 5. У такой «идеальной» пирамиды (рис. 2) осевое сечение составлено из двух «священных» египетских треугольников [прим. 1].
В её основании лежит квадрат со стороной 6 (3+3). Высота равна 4, угол наклона боковых граней 53,08°, а угол наклона рёбер к основанию - 43,19°. Объём пирамид вычисляется по формуле V = 1/3*S*H (где S - площадь основания, а Н - высота пирамиды) и равняется у «идеальной» 48. Великие пирамиды, имеющие высоту (со «срезанной» верхушкой) от 62 до 150 метров, разумеется, незначительно отличаются от «идеальной». При этом во время строительства пирамиды Хефрена была допущена погрешность угла её наклона на четыре минуты (!), что уменьшило высоту пирамиды (по сравнению с расчётной идеальной) всего на 20 см. И это при высоте пирамиды 143,5 м! Современные строители, используя строительную технику и измерительные приборы, вряд ли справились бы с поставленной задачей более успешно. Российские пирамиды (фото 5) имеют иную геометрию. Их идеологи-архитекторы и строители - наши современники, поэтому ответы на многие вопросы лежат рядом, на поверхности, а не за морями-океанами в глубине веков. Достоверно известно, что в устройство современных пирамид заложена пропорция «золотого сечения» [прим. 2]. Представьте себе построение (вроде снеговика), состоящую из нескольких шаров - один сверху другого (рис. 1), а вплотную к шарам, по бокам, четыре треугольных щита, образующих пирамиду. Диаметры соседних шаров соотносятся в пропорции «золотого сечения» [прим. 3]. Разумеется, внутри современных пирамид нет никаких шаров - они полностью полые (если не считать любознательных посетителей, желающих заглянуть в тайны мироздания или приобщиться к законам гармонии). Гиды рассказывают (а средства массовой информации повторяют) об удивительных свойствах этих пирамид. Вернее, явлениях, которые якобы возникают внутри таких пирамид и ближайших окрестностях. Например, автор этих строк видел пластиковую бутылку с обычной минеральной водой (в заводской упаковке), которая не замерзала внутри пирамиды даже при сильном морозе. Достаточно было по такой бутылке резко ударить рукой, и бурный процесс кристаллизации происходил буквально на глазах. Вода превращалась в лёд! Зрелище, безусловно, впечатляющее. Не меньшие детские впечатления остались у меня от опытов с водой моего деда - Акима Тимофеевича, которые он проводил на Крещение. Пирамиды у входа в Лувр (Париж), различные башенки на крышах коттеджей «новых русских», офисных зданиях, в палатках с сувенирами... просто всеобщее помешательство. Зачем строили пирамиды? Зачем их строят сейчас? Предлагаем вам сложить несколько пирамид из бумаги, и быть может, эти вопросы обретут иной смысл. Андрей Никулин, Москва
Фото 5
	Москва. Пушкинская площадь.
1) Это единственный треугольник, стороны которого образуют арифметический ряд. Сакральный вид имеет не только эта последовательность, теорема Пифагора (3^2+4^2=5^2), но и то, что кубическое число площади такого треугольника (6) равно сумме кубических чисел его сторон (6^3=3^3+4^3+5^3). За прямоугольным треугольником с соотношением сторон 3:4:5 закрепилось название «священного» египетского - сумма его сторон равняется числу 12 (самому популярному числу всех времён и народов). 2) Под названием "золотое сечение», «золотое деление» или даже "божественное деление» у древних геометров было известно деление «в крайнем и среднем отношении». Разделить данную величину (например, число или отрезок) «в крайнем и среднем отношении» - значит разделить её на такие две неравные части, чтобы большая относилась к меньшей, как вся величина относится к большей части. 3) Математическая особенность «золотого сечения» заключается в том, что эта пропорция связывает между собою отношения частей и целого. В количественном выражении ряд "золотого сечения» может быть представлен следующим образом; ... 0,056; 0,090; 0,146; 0,236; 0,382; 0,618; 1; 1,618; 2,618; 4,237; 6,856... и т. д. Значения эти приблизительные. Каждое последующее число ряда можно получить, умножив (разделив) предыдущее на 0,618 (а в точном выражении - на значение корня из 5 - 1 /2). Весь этот ряд состоит из иррациональных чисел. В тоже время каждое последующее число в нём равно сумме двух предыдущих.
⇨: Соробан – японский деревянный компьютер	⇦: О лягушках		⇧ (Оглавление № 27)