Оригами № 2(17) 1999
Круг
В этой рубрике журнала мы договорились называть красивыми пропорциями, или форматами, такие, которые являются наиболее гармоничными, соответствующими природным пропорциям и пропорциям человека, его восприятию и ощущениям. Геометрическими фигурами, наиболее полно выражающими этот принцип, принято считать круг, квадрат, прямоугольник, треугольник и правильный пятиугольник. В этом номере мы постараемся разглядеть красоту и пропорциональность круга и изделий оригами, выполненных из него.
Окружность древние греки считали самой совершенной из всех геометрических фигур за её удивительно гармоничные свойства — все точки окружности расположены на одинаковом расстоянии от её центра. Именно поэтому окружность — единственная фигура (в т.ч. и среди кривых), которая может «скользить сама по себе», вращаясь вокруг центра. Это свойство окружности легло в основу одного из величайших изобретений человечества — колеса. Возьмите нитку произвольной длины и свяжите её концы. Положив на стол, сделайте из неё окружность, а затем любой многоугольник (квадрат, треугольник и т.д.). Площадь, ограниченная окружностью (т.е. площадь круга), — наибольшая среди возможных из полученных таким образом площадей. Кроме того, говоря о площадях каких-либо других фигур, обычно говорят: «площадь квадрата» или, например, «площадь пятиугольника», но не площадь, ограниченная квадратом. Таким образом, введя два понятия — окружность и круг, наши предки особо выделили значимость удивительно гармоничной фигуры. Для изучения другого замечательного свойства окружности нам понадобится лист тонкой, прозрачной бумаги (лучше всего кальки). Проделайте последовательно действия:
1. Нарисуйте окружность на листе прозрачной бумаги. Обозначьте центр окружности буквой - О. Выберете внутри окружности произвольно точку А, отличную от центра окружности. Перегните лист бумаги так, чтобы точка А оказалась на окружности. Задание имеет множество решений, поэтому перегните лист бумаги несколько раз. Всякий раз точка А должна попадать на окружность. При достаточно большом количестве перегибов можно убедиться в том, что каждая линия сгиба касается эллипса. Эллипс будет «проявляется» как огибающая касательных. Точки О и А являются фокусами этого эллипса.					Вписание греческими ремесленниками в круг квадрата и равностороннего треугольника для гармонизации произведения
Подобным образом можно построить гиперболу и параболу, расположив точку А на окружности или вне неё. Таким простым способом, путём складывания прозрачного листка бумаги, легко убедиться во взаимосвязи этих кривых. Окружность при этом является как бы прародительницей эллипса, гиперболы и параболы. Все четыре кривые (окружность, эллипс, гипербола и парабола) являются коническими сечениями. Других «правильных» кривых в природе нет. А сколько различных вариантов выбора месторасположения точки А? Очевидно, что тоже четыре (в центре окружности, внутри окружности, на самой окружности и вне неё). 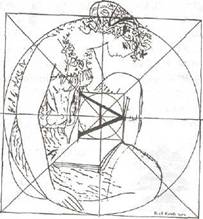Задача о квадратуре круга — одна из самых знаменитых задач древности. Построить с помощью циркуля и линейки квадрат, площадь которого равнялась бы площади данного круга, пытались на протяжении четырёх тысячелетий. Только в 1882 г. немецкий математик Ф.Линдеман доказал, что с помощью циркуля и линейки эту задачу решить невозможно. А при помощи оригами? Вопрос пока остаётся открытым... Решим более простую задачу, связанную с квадратом и кругом. Для этого сделаем построения: Из листа бумаги вырежем круг. Впишем в него квадрат. Для этого разделим окружность на четыре равные части, а затем перегнём по хордам. В получившийся квадрат впишем ещё один — поменьше. Углы меньшего квадрата должны находиться посередине сторон большого квадрата Задача: Если радиус круга равен 1, чему будет равна сторона меньшего квадрата? (Ответ) Пытаясь объяснить строение Вселенной исходя из принципов целесообразности и красоты, И. Кеплер брал за основу правильные многогранники и окружность. Размышления Кеплера относительно строения солнечной системы, в итоге приведшие к знаменитым «законам Кеплера», начинались с попытки (оказавшейся неудачной) связать само число известных к тому времени планет Солнечной системы, а также расстояние этих планет от Солнца с пятью правильными многогранниками. (Невооружённым глазом с Земли можно наблюдать только пять планет!) Его первые и ошибочные рассуждения заключались в следующем: орбиты всех планет расположены на сферах, которые последовательно вписаны в одни правильные тела и описаны вокруг других, — вроде того, как у нас на плоскости в последней задаче.
Окружности и её части — дуги являются обязательными элементами в архитектуре различных эпох и стилей. Красота и пропорциональность окружности, как совершенной геометрической формы, привлекала к себе внимание художников и
			Образцы некоторых древних семейных гербов японцев
архитекторов с древнейших времён. Окружности, дуги, различные арки являются не просто частями конструкции, а придают «воздушность» торжественность и «лёгкость» всему архитектурному ансамблю. Для проектирования архитектурных деталей и сооружений круговой формы древние зодчие использовали деление целого эталона на 21 элемент. Поскольку при любых размерах круга, если его диаметр разделить на 21 часть, то на самой окружности с большой точностью будет укладываться 66 таких же отрезков (C=27iR=rcD; 66:21=3,1428....). Соответственно цифры 21 и 66 приобрели особый, мистический оттенок...				Дмитровский собор в городе Владимире, XII век
Циферблат часов поделён на 12 равных частей. Почему именно 12? Достоверно известно, что египетские геометры («гарпедонаптаи» — натягиватели верёвок) в качестве измерительного инструмента использовали верёвку, поделенную узлами на 3/12,4/12 и 5/12 частей своей длины. Попробуйте самостоятельно разделить верёвку в таких пропорциях путём складывания. Есть (или нет) между делением окружности и верёвки на 12 равных частей какая-либо взаимосвязь? Поразмышляйте на эту тему. В создании орнаментов часто используются окружности.				Елецкое кружево (кружевной промысел возник во многих сёлах и деревнях близ Ельца в начале XIX века)
«Кусудамы — волшебные шары» рождались в одном из приложений к нашему журналу из отдельных частей-модулей, каждый из которых в свою очередь складывался из квадратика бумаги. Быть может, используя в качестве исходного формата круг, можно тоже получить красивые и гармоничные оригами? Моделей оригами из круга пока известно не так много. Для складывания своих собственных оригами из круга вам может понадобиться разделить его на равные части — об этом заметка В.Гончар.
Товарные знаки некоторых автомобильных фирм
А в заключение несколько вопросов, над которыми задумайтесь в часы досуга: почему стержень шариковой ручки в поперечном сечении имеет форму круга? (аналогично — одножильный провод, стержень карандаша, люминесцентная лампа, бутылка...); почему железные крышки водо-канализационных люков круглые? почему монеты и медали круглые, а ордена нет? почему говорят «круглый дурак» (или, наоборот «круглый отличник»), а не, например «квадратный»? «круговая порука» — это, наверное, не то же самое, что «любовный треугольник»? Посмотрите по сторонам, таких «почему» вы сможете задать себе и нам много. Напишите о своих размышлениях на этот счёт. А может быть, кто-то попытается сложить (известные и новые) базовые формы и модели не из квадрата, а из круга? Андрей НИКУЛИН Ответ к задаче: сторона меньшего квадрата равна радиусу круга.
⇨: Корейские ребята		⇦: Томас Халл			⇧ (Оглавление № 17)